a方加b方等于什么,a的立方加b的立方等于多少
发布:小编
本文目录
a的立方加b的立方等于多少?
a³+b³=(a+b)(a²-ab+b²)
解题过程:
一、加一项减一项,保证等式两边不变
=a²a-a²b+ab²+a²b-ab²+b³
二、提取公因数
=a(a²-ab+b²)+b(a²-ab+b²)
三、提取公因式
=(a+b)(a²-ab+b²)
四、得出结论
a³+b³=(a+b)(a²-ab+b²)
相关内容:
①完全立方公式:
完全立方公式包括完全立方和公式和完全立方差公式,完全立方和(或差)公式指的是两数和(或差)的立方等于这两个数的立方和(或差)与每一个数的平方乘以另一个数3倍的和(或差),即(a±b)^3=a^3±3a^2 b+3a b^2±b^3。
②变形(常用)立方公式:
(1)立方和:a³+b³=(a+b)(a²-ab+b²)
(2)立方差公式a³-b³=(a-b)(a²+ab+b²)
(3)三数和平方公式(a+b+c)²=a²+b²+c²+2ab+2ac+2bc
③立方差公式与立方和公式统称为立方公式,两者基本描述如下 :
立方和公式,即两数立方和等于这两数的和与这两数平方和与这两数积的差的积。也可以说两数立方和等于这两数积与这两数差的不完全平方的积 。
扩展资料:
(a+b)^n=(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)b+...+C(n,r)a^(n-r)b^r+...+C(n,n)b^n。
依据:(二项式定理的应用)
1、二项式定理(英语: Binomial theorem),又称 牛顿二项式定理,由 艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如 展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂,即 广义二项式定理。
2、它不是一个等差数列,也不是一个 等比数列,但通过二项式定理的展开式,可以转化为按等差数列,由低次幂到高次幂递进求和,最终可推导至 李善兰 自然数幂求和公式的原形。
3、所有添加的二项式展开式数,按二项式展开式确定,如此可以顺利进行自然数的1至n幂的求和公式的递进推导,最终可以推导至 李善兰 自然数幂求和公式。
立方差公式,即两数立方差等于这两数差与这两数平方和与这两数积的和的积。也可以说,两数立方差等于两数差与这两数和的不完全平方的积 。
参考资料:
a立方加b立方等于什么公式
=(a+b)*(a^2+b^2-a*b) 这是立方和公式a^3+b^3=(a+b)*(a^2+b^2-a*b) ,可以类比有a^3-b^3=(a-b)*(a^2+b^2+a*b)
记得采纳啊
a方加b方等于什么公式
a方加b方的公式:如果是勾股定理,在直角三角形中,两条直角边分别为a、b,斜边为c,则a^2+b^2=c^2;如果是因式分解:a^2+b^2=(a+b)^2-2ab=(a-b)^2+2ab。
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
a平方加b平方等于多少
a平方加b平方等于(a+b)2-2ab。两个字母的平方之间的关系时,通常会考虑平方差和完全平方公式,而题目是相加的形式,所以我们就锁定完全平方公式。其次,我们知道(a+b)²=a²+b²+2ab,所以把2ab移到左边就可以知道答案了。
这是一个完全平方公式,两数和的平方,等于它们的平方和加上它们的积的2倍。该公式是进行代数运算与变形的重要的知识基础,是因式分解中常用到的公式。该知识点重点是对完全平方公式的熟记及应用。难点是对公式特征的理解,如对公式中积的一次项系数的理解等。

完全平方公式学习方法
两数和或差的平方,等于它们的平方和,加上或减去它们的积的2倍。叫做完全平方公式.为了区别,我们把前者叫做两数和的完全平方公式,后者叫做两数差的完全平方公式。左边是两个相同的二项式相乘,右边是三项式,是左边二项式中两项的平方和,加上或减去这两项乘积的2倍。
左边两项符号相同时,右边各项全用加号连接,左边两项符号相反时,右边平方项用加号连接后再减两项乘积的2倍。公式中的字母可以表示具体的数正数或负数,也可以表示单项式或多项式等数学式。
以上就是关于a方加b方等于什么,a的立方加b的立方等于多少的全部内容,以及a方加b方等于什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。
大家都在看
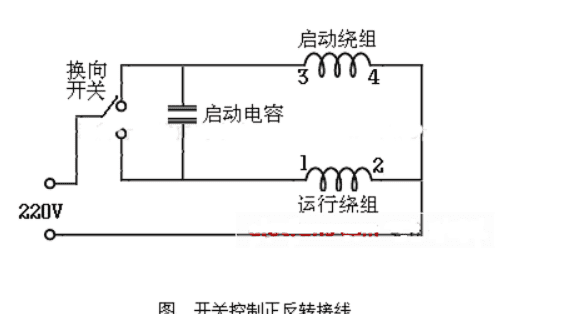
换气扇电容怎么接线,换气扇用电动机接线方法
综合百科换气扇电容怎么接线1、从电机出来三根线,红黑黄。2、分别量下红黑红黄黑黄这三组直流电阻。3、这三个组阻值是代数和关系。4、比如红黑20欧红黄50欧黑黄就是70欧(把最大阻值这两根线除去,剩下的那根称为公共端,这时红的是公共端)。5、电阻没有一样时,表示只能往一个方向转。6、公共端
产权比率是怎么算出来的,产权比率怎么计算
综合百科本文目录1.产权比率怎么计算2.产权比率的计算公式是什么意思3.共有产权房产权比例怎么计算4.共有产权房产权比例怎么计算产权比率怎么计算产权比率计算公式一般是:负债总额/股东权益的。还有其他几种的计算方式的,一般产权都是高风险高回报的,是对于资本结构的一种合理稳定的反映,对于房产

高压锅烧碳化了怎么洗,高压锅烧焦了怎么去除焦味
综合百科高压锅烧碳化了怎么洗高压锅烧碳化了的清洗方法:在锅里放水浸泡,加入几滴白醋,泡几个小时就好了,或者加热一下效果会更理想。高压锅又叫压力锅,压力煲,是一种厨房的锅具。压力锅通过液体在较高气压下沸点会提升这一物理现象,对水施加压力,使水可以达到较高温度而不沸腾,以加快炖煮食物的效率。

对公账户有没有银行卡,对公账户有银行卡号吗
综合百科对公账户有没有银行卡对公账户是有银行卡的,但是银行卡不能在ATM机上操作,它一般取现要去开户行的柜台进行,而对公账户的交易也是通过支票、转账等形式完成,不需要用银行卡在ATM上操作。但现在对公账户一般不办理银行卡的,但有一些国有银行和个别非国有银行出现了对应于中小企业的对公银行卡

外科口罩和医用防护口罩的区别,医用外科口罩和医用防护口罩有什么区别
综合百科本文目录1.医用外科口罩和医用防护口罩有什么区别?2.外科灭菌口罩和医用外科口罩哪个好3.外科口罩和医用防护口罩的区别外科口罩和n95口罩的区别外科口罩佩戴方法4.医用外科口罩什么品牌质量好医用外科口罩和医用防护口罩有什么区别?1、过滤等级不同医用护理口罩用于阻隔口腔和鼻腔呼出的

百香果整个冷冻行,百香果可以放冰箱冷藏保存多久
综合百科本文目录1.百香果可以放冰箱冷藏保存多久2.百香果可以带壳冷冻保存吗3.百香果吃不完可以冷冻吗4.百香果直接冷冻可以存放多久百香果可以放冰箱冷藏保存多久1、百香果可以放冰箱。2、百香果在保存的时候可以将百香果用保鲜膜一个个包好后放在冰箱的冷藏室里,这样可以存放一个星期左右,不过吃

微信说话时间太短是怎么回事,手机微信发语音时间太短怎么回事啊
综合百科微信说话时间太短是怎么回事我们常遇见这样的问题,在微信中发送语音消息经常只能发送10秒,这与您的按压有关,请您在录制语音的时候尝试加大按压力度,且不能移动自己的手指,这样就能发送大于10秒的语音消息了。微信使用技巧:1、朋友圈快速回到顶部--首先打开微信App并进入朋友圈页面,向

唐僧的金句,谁可以告诉我大话西游里的唐僧经典语录
综合百科本文目录1.谁可以告诉我大话西游里的唐僧经典语录呢2.大话西游里唐僧的经典台词语录3.唐僧名言经典语录我自东士大4.《西游记》唐僧女儿国的经典语录有哪些谁可以告诉我大话西游里的唐僧经典语录呢观音:孙悟空,你这个畜牲,你本来答应如来佛祖护送你师傅唐三藏去取西经的,你居然跟牛魔王串通

如何把鸡蛋立在桌子上,怎么才能使鸡蛋竖立于桌面呢
综合百科如何把鸡蛋立在桌子上把鸡蛋立在桌子上需要立鸡蛋的手尽量保持不动,让蛋黄可以慢慢沉淀到鸡蛋下部,这样重心就能足够低,使鸡蛋保持平衡。一旦重力作用线能经过这个平面,鸡蛋就能站立起来。还可以将鸡蛋的重心放到上面,这样鸡蛋就可以立起来了,这样重心会比较低,就像不倒翁一样,容易保持平衡。

移动手机可以插电信的卡可以用,移动版手机可以用电信卡
综合百科本文目录1.移动版手机可以用电信卡吗2.电信卡移动手机能用吗3.移动手机能用电信卡吗?4.电信手机卡放在移动手机里能不能用移动版手机可以用电信卡吗不可以,移动手机是不支持电信cdma网络制式的,所以是不能安装电信手机卡使用的,电信手机卡只能安装在支持电信制式的手机中使用。电信卡移

缩短水沸腾时间的方法,缩短加热时间使水尽快沸腾的方法
综合百科缩短水沸腾时间的方法1、减小液体表面气压,降低液体沸点;2、提高水的初温;3、减少需加热的水的质量;4、减少热量的散失,如加盖子、用隔热效果好的容器;5、改进加热方式,用热值较好的燃料等。沸腾是指液体受热超过其饱和温度时,在液体内部和表面同时发生剧烈汽化的现象。不同液体的沸点不同

严重贫血怎么办,贫血怎么办
综合百科本文目录1.贫血怎么办2.贫血怎么办3.贫血怎么治最快最有效4.贫血怎么办贫血怎么办贫血虽然说是一种常见症状,一般的贫血可进行饮食调理,如果症状比较严重,可适当服用药物治疗;若是某些疾病引起,则需要积极的治疗原发病。一、饮食调理1.多吃蛋白质丰富的食物:贫血患者一定要多吃些蛋白质








