勾股定理证明方法，勾股定理的证明方法

勾股定理证明方法

1、勾股定理证明方法：以ab为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于2分之一ab。AEB三点在一条直线上，BFC三点在一条直线上，CGD三点在一条直线上。证明四边形EFGH是一个边长为c的正方形后即可推出勾股定理。

2、勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理的证明方法

简单的勾股定理的证明方法如下：

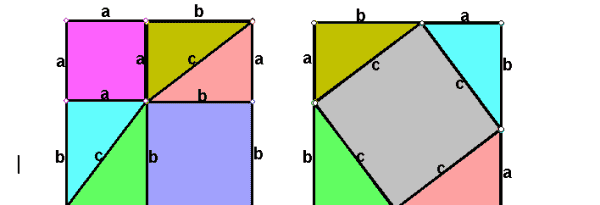
做8个全等的直角三角形，设它们的两条直角边长分别为碰游a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，段神把它们像上图那样拼成两衫袜雹个正方形。

发现四个直角三或帆角形和一个边长为a的正方形和一个边长为b的正方形，刚好可以组成边长握吵亏为（a+b）的正方形；四个直角三角形和一个边长为c的正方形也刚好凑成边长为（a+b）的正方形。

所以可以看出以上两个大正方形面积相等。 列出式子可得：

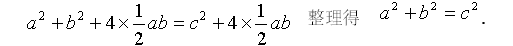
拓展资料：

勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最好模重要的工具之一，也是数形结合的纽带之一。在中国，商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。

参考资料：勾股定理_百度百科

勾股定理的最简单的证明方法是什么

简单的勾股定理的证明方法如下：

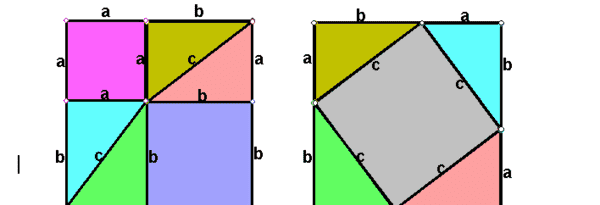
拓展资料：

勾股定理的使用方法：

1、确保三角形是直角三角形。 勾股定理只适用于直角三角形中，所以，在应用定理之前，你需要先确定三角形是否是直角三角形，这一点非常重要。幸好，区分直接三角形和别的三角形的方法只有一个，那就是看一个三角形中是否有一个90度的角。

2、确定变量a，b，c对应的三角形的边。在勾股定理中，a，b表示直角三角形的两条直角边，而c用来表示斜边，即直角对应的那条最长的边。所以，先给两条直角边分别标注上a，b（具体的对应关系没有要求），而斜边标注上c。

3、确定你所要求的边。使用勾股定理可以求出直角三角形的任意一条边的长度，但前提是知道另外两条边的长度。先确定哪一条边的长度是未知的——a，b或者c。

4、代入。将两条已知边的长度带入到公式a2 + b2 = c2中，其中a和b对应的是两直角边的长度，而c代表斜边长度。在上面的例子中，我们知道一条直角边和斜边的长度（3和5），然后将3和5代入到公式中，有32 + b2 = 2。

5、计算平方。首先，计算两条已知边长度的平方值。或者，你也可以先不计算出来，然后保留平方，带到式子中直接计算平方和。在上述例子中，3和5的平方分别是9和25，所以方程可以改写为9 + b2 = 25。

6、将未知变量移到等号一边。如果有必要的话，运用基本的代数操作，将未知变量移动到等号一侧，而将已知变量移动到等号的另一侧。如果你要求的是斜边长，那么就不需要再移动变量了。在上述例子中，方程式是9 + b2 = 25。两边同时减去9，等式变为b2= 16。

7、求开方。现在等式两边一边是数字，另一边是变量，然后同时求两边的平方根。在上述例子中b2 = 16，两边同时求平方根，有b = 4。因此，未知边的长度就是4。

以上就是关于勾股定理证明方法，勾股定理的证明方法的全部内容，以及勾股定理证明方法的相关内容,希望能够帮到您。

版权声明：本文来自用户投稿，不代表【推酷网】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：350149276@qq.com）我们将及时处理，共同维护良好的网络创作环境。