勾股定理证明方法,勾股定理有哪些证明方法初中
发布:小编
本文目录
勾股定理有哪些证明方法初中
几何证明法:这是最常见、最流行的证明方法。这种方法的核心思想是通过将直角三角形拆分成若干个图形,利用形状相似、面积相等等几何条件,最终证明勾股定理成立。代数证明法:通过代数方法对勾股定理进行证明,这种方法通常依赖于一些数学前提知识。例如,经典的代数证明法包括使用勾股定理推导出正弦、余弦函数的关系等。
向量证明法:这种方法利用了向量的数学性质,将勾股定理转换成向量论著名的“勾股定理”,然后通过向量的几何性质得出勾股定理。三角函数证明法:这种方法将三角函数和勾股定理联系起来进行证明。例如,可以通过正切函数的周期性和相应角度的三角函数关系等得到勾股定理。
微积分证明法:这种方法依赖于微积分的知识,通过对函数的导数和极限进行推导,最终得出勾股定理。平面几何证明法:该方法主要是运用平面几何的基本公理和定理对勾股定理进行证明。例如,可以通过直线平行公设、圆的性质、四边形的性质等等,来推导证明勾股定理。
对偶证明法:这种方法有点特殊,它并不是直接证明勾股定理的。它相当于对勾股定理的形式进行逆转,然后对逆转后的形式进行证明。具体来说,可以将勾股定理中三条边分别变成三条边上的高,然后重新组合成一个三角形,通过证明这个三角形是等腰直角三角形,从而推导出勾股定理的成立。
同时可以提到的是,在不同的场景中,勾股定理还有更多的证明方法,如利用切线、反演、射影几何等等。虽然证明方法很多,但无论是哪种方法,都能让我们深入地理解勾股定理,并应用到更广泛的数学领域中。总之,不同的证明方法各具特色,可以从不同的角度去理解和应用勾股定理。
勾股定理怎么证明
简单的勾股定理的证明方法如下:

做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形。
发现四个直角三角形和一个边长为a的正方形和一个边长为b的正方形,刚好可以组成边长为(a+b)的正方形;四个直角三角形和一个边长为c的正方形也刚好凑成边长为(a+b)的正方形。
所以可以看出以上两个大正方形面积相等。 列出式子可得:

拓展资料:
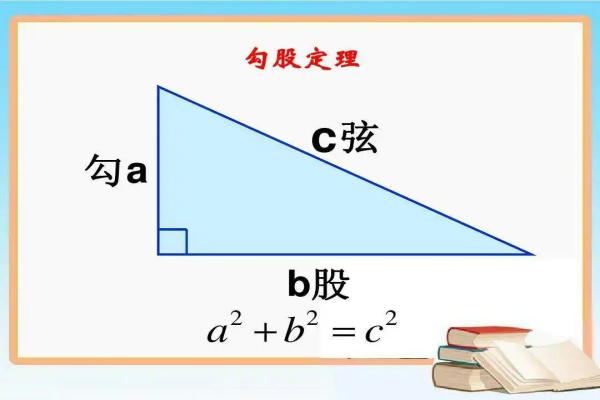
勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例。在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
参考资料:
勾股定理的四种证明方法初二
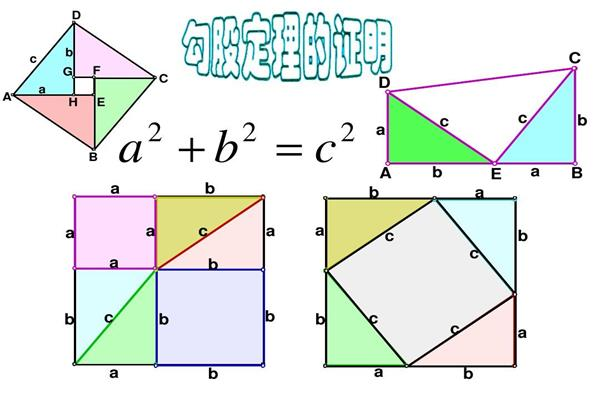
勾股定理的四种证明方法有加菲尔德证法,赵爽弦图,青朱出入图,欧几里得证法。

1、加菲尔德证法。
加菲尔德在证出此结论5年后,成为美国第20任总统,所以人们又称其为总统证法。在直角梯形ABDE中,加菲尔德证法变式该证明为加菲尔德证法的变式。如果将大正方形边长为c的小正方形沿对角线切开,则回到了加菲尔德证法。相反,若将上图中两个梯形拼在一起,就变为了此证明方法。

2、赵爽弦图。
勾股各自乘,并之为玄实。开方除之,即玄。案玄图有可以勾股相乘为朱实二,倍之为朱实四。以勾股之差自相乘为中黄实。加差实亦成玄实。以差实减玄实,半其余。以差为从法,开方除之,复得勾矣。加差于勾即股。凡并勾股之实,即成玄实。或矩于内,或方于外。形诡而量均,体殊而数齐。勾实之矩以股玄差为广,股玄并为袤。

3、青朱出入图。
青朱出入图,是东汉末年数学家刘徽根据割补术运用数形关系证明勾股定理的几何证明法,特色鲜明、通俗易懂。刘徽描述此图,勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂。开方除之,即弦也。其大意为,一个任意直角三角形,以勾宽作红色正方形即朱方,以股长作青色正方形即青方。

4、欧几里得证法。
在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ABC为一直角三角形,其中A为直角。从A点划一直线至对边,使其垂直于对边。延长此线把对边上的正方形一分为二,其面积分别与其余两个正方形相等。在这个定理的证明中,我们需要如下四个辅助定理:如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。
勾股定理的证明方法
勾股定理的证明方法:
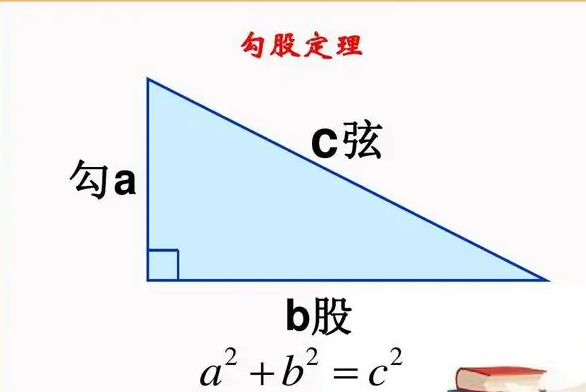
1、以a b为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于2分之一ab。
2、AEB三点在一条直线上,BFC三点在一条直线上,CGD三点在一条直线上。
3、证明四边形EFGH是一个边长为c的正方形后即可推出勾股定理。
勾股定理的意义
1、勾股定理的证明是论证几何的发端。
2、勾股定理是历史上第一个把数与形联系起来的定理,即它是第一个把几何与代数联系起来的定理。
3、勾股定理导致了无理数的发现,引起第一次数学危机,大大加深了人们对数的理解。
4、勾股定理是历史上第一个给出了完全解答的不定方程,它引出了费马大定理。
5、勾股定理是欧氏几何的基础定理,并有巨大的实用价值。这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在高等数学和其他科学领域也有着广泛的应用。1971年5月15日,尼加拉瓜发行了一套题为“改变世界面貌的十个数学公式”邮票,这十个数学公式由著名数学家选出的,勾股定理是其中之首。
以上就是关于勾股定理证明方法,勾股定理有哪些证明方法初中的全部内容,以及勾股定理证明方法的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。
大家都在看

张子枫高考成绩391是真的吗,张子枫资料 她取得了什么成就
综合百科张子枫资料 她取得了什么成就1、张子枫,2001年8月27日出生于河南省三门峡市,中国内地女演员。2、在5岁时,张子枫开始拍广告并因参演多部电视剧从而进入演艺圈。2009年,凭灾难情感片《唐山大地震》的“小方登”一角而崭露头角,并获得第31届大众电影百花奖最佳新人奖。3、2017

想通过法律援助离婚可以,离婚可以申请法律援助律师
综合百科本文目录1.离婚可以申请法律援助律师吗2.离婚可以法律援助吗3.离婚能申请法律援助吗?4.法律援助中心可以咨询离婚吗离婚可以申请法律援助律师吗法律分析:1、各地收费标准不同,实际收费可能在几百元直至数万元不等,这与夫妻共同财产的多少有直接关系;2、如果因为家庭生活困难,则可以申请

转账开户行错误能转过去,开户行写错了能转账成功多久退回
综合百科转账开户行错误能转过去吗?开户行写错时,如果只是写错开户行名称中支行名称的部分,而且错误填写的支行和实际支行处于同一城市,那么转账是可以成功的。如果是上面提到这种情况的以外情况,则转账会失败,该笔转账金额将在第二天退回到出款账户。 开户行写错了能转账成功多久退回开户行写错时,如
gpu驱动是什么,adreno 630 gpu driver模块
综合百科本文目录1.adreno 630 gpu driver模块2.gpu驱动程序怎么升级3.显卡的驱动叫什么名字4.gpu驱动是什么意思adreno 630 gpu driver模块adreno630GPUdriver模块就是adreno630的GPU驱动。gpu驱动是图形处理器,又

苹果手机怎么会突然黑屏,苹果手机突然黑屏怎么回事
综合百科苹果手机怎么会突然黑屏1、开机线路不正常:使用外接电源给手机供电,使用电联表检测看看示数是否有变化,如果没有变化的话很可能就是开机线断了或者开机键接触不良。2、电池的供电电路不正常:使用外部接口对手机进行供电,看看开机时候恢复正常,如果正常的话就确定是手机的供电电路不正常。3、手

a2223和a227区别,苹果x能装双卡槽吗
综合百科a2223和a2217区别以苹果iPhone11pro为例,其实a2220和a2217除了生产批号不同,其它功能各方面都是一样的。iPhone11Pro是美国Apple(苹果公司)第一支命名为Pro的手机,采用后置三摄设计,配色有暗夜绿、太空灰、银白色和金色四款。北京时间2019

做梦跑不动是怎么回事,做梦梦见自己跑步跑不动迈不开
综合百科本文目录1.做梦梦见自己跑步跑不动,迈不开2.为什么有时候跑步感觉很累3.为什么有时候跑步感觉很累4.梦见跑步跑不动是什么意思做梦梦见自己跑步跑不动,迈不开梦见跑步跑不动:人际关系运气较好。如有困难,必有长辈来帮忙。如果你与情人的关系不太如意,不妨向长辈请教该如何应付。待业者梦见
手机一直正在搜索怎么回事,为什么手机一直显示在录音
综合百科手机一直正在搜索怎么回事手机一直正在搜索是因为网络故障无法完成搜索任务,强制关闭启动搜索的应用即可恢复正常。手机全称为移动电话或无线电话,通常称为手机,原本只是一种通讯工具,早期又有大哥大的俗称,是可以在较广范围内使用的便携式电话终端。手机分为智能手机和非智能手机,一般智能手机的

死刑执行要有判决书,死刑犯判决书下达后多久执行
综合百科死刑执行要有判决书吗?死刑犯执行前必须有判决书,没有判决书的死刑犯,被执行了死刑,就等同于故意杀人。【法律依据】《刑事诉讼法》第二百三十五条,死刑由最高人民法院核准。第二百三十六条,中级人民法院判处死刑的第一审案件,被告人不上诉的,应当由高级人民法院复核后,报请最高人民法院核准。

洛阳市社会医疗保险卡在哪里缴费,洛阳居民医保缴费怎么网上缴费的
综合百科本文目录1.洛阳居民医保缴费怎么网上缴费的2.洛阳城镇居民医保首次怎么网上缴费的呢3.2020洛阳居民医保网上缴费4.外地人怎么在当地交医保洛阳居民医保缴费怎么网上缴费的法律主观:如今是一个法制的社会,很多与生活息息相关的事情都离不开法律,所以我们对一些平常的法律知识应该有所认识
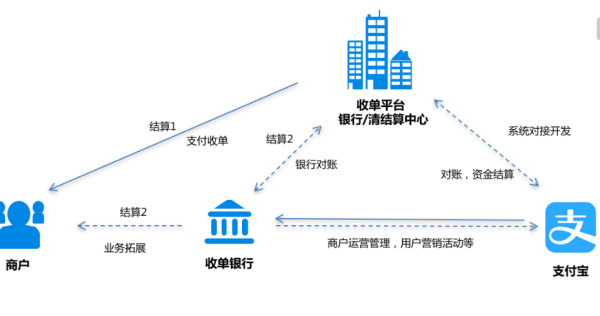
全国银行卡中心商户什么意思,银行网点名称是什么意思
综合百科本文目录1.银行网点名称是什么意思2.银行卡的收单业务是什么意思3.中国银行商户通业务4.中国银联什么意思银行网点名称是什么意思银行网点就是银行对外营业的地方,一般分为总行,支行、储蓄所和二十四小时自助银行等。简单来说就是银行的营业厅,各大银行的总部分支出来的业务地点,为了方便全

环境温度传感器在哪里,东风天龙环境温度传感器装什么位置
综合百科环境温度传感器在哪里汽车发动机的环境温度传感器一般都安装在水箱的前面,在汽车保险杠的前面。环境温度传感器是用来检测汽车环境温度的高低的装置,汽车上的控制系统会根据车外的温度与车内温度进行对比,然后决定控制方式,环境温度传感器会给ECU提供汽车外的温度信号,ECU会根据这个信号控制






