四边形如何分类，如何区分四边形和平行四边形

四边形如何分类

四边形定义：由不在同一直线上四条线段依次首尾相接围成的封闭的平面图形或立体图形叫四边形，由凸四边形和凹四边形组成，并且顺次连接任意四边形上的中点所得四边形叫中点四边形，中点四边形都是平行四边形；也就是说，四边形分凸四边形和凹四边形；凸四边形分为一般凸四边形和梯形、平行四边形；平行四边形又分为普通平行四边形，矩形，菱形，正方形。

如何区分四边形和平行四边形

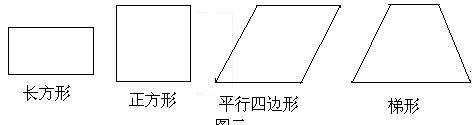
四边形，平行四边形，长方形，正方形，梯形之间的关系为：

1、以上图形均为四边形，都是由不在同一直线上的不交叉的四条线段依次首尾相接围成的封闭的平面图形。

2、长方形、正方形是特殊的平行四边形，除了具有两组对边分别平行的特征之外，还具有四个内角都为直角的特征。

3、正方形是特殊的长方形，因为其四条边长度都相等。

4、平行四边形是两组对边分别平行的四边形，而梯形是只有一组对边平行，另一组对边不平行的四边形。

5、平行四边形、长方形、正方形、梯形的面积计算均为底边与对应的高相乘。

6、平行四边形，长方形，正方形，梯形均为凸四边形，内角和和外角和均为360度。

扩展资料

四边形中除了平行四边形，长方形，正方形，梯形等凸四边形之外，还有凹四边形。

凹四边形四个顶点在同一平面内，对边不相交且作出一边所在直线，其余各边有些在其异侧。

凹四边形区别于凸四边形的地方在于：有且仅有一个角大于180°,但小于360°;其余三个角中,与最大角相邻的两个角一定是锐角。(最大角的对角可以是锐角,直角或钝角.其外角等于其他三个内角之和。)。

四边形是怎么分类的图画

根据两边的平行程度分类。四边形分凸四边形和凹四边形，其中凸四边形是指作出一边所在直线，其余各边均在其同侧；凸四边形的内角和和外角和均为360度；凹四边形是指作出一边所在直线，其余各边在其异侧。凸四边形分为一般凸四边形和梯形、平行四边形，平行四边形又分为普通平行四边形、矩形、菱形和正方形。

四边形的种类有哪几种图片大全

五种，四边形的种类：

(一)平行四边形

1、定义：两组对边分别平行的四边形叫做平行四边形。

2、性质：

(1)平行四边形的面积等于底和高的积。

(2)如果一个四边形是平行四边形，那么这个四边形的两组对边、两组对角分别相等。

(3)如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。

(4)如果一个四边形是平行四边形，那么这个四边形的邻角互补。

(5)平行四边形不是轴对称图形，但平行四边形是中心对称图形。

(二)矩形

1、定义：矩形是至少有三个内角都是直角的四边形。矩形是一种特殊的平行四边形，矩形也叫长方形。

2、性质：

(1)有一个角是直角的平行四边形是矩形;

(2)对角线相等的平行四边形是矩形。

(3)有三个角是直角的四边形是矩形。

(4)定理：经过证明，在同一平面内，任意两角是直角，任意一组对边相等的四边形是矩形。

(5)对角线相等且互相平分的四边形是矩形。

(三)正方形

1、定义：有一组邻边相等并且有一角是直角的平行四边形叫做正方形，正方形是特殊的平行四边形。

2、性质：

(1)正方形的四个角都是直角，四条边都相等;

(2)正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角。

(3)正方形既是中心对称图形，又是轴对称图形(有四条对称轴)。

(四)菱形

1、定义：在同一平面内，有一组邻边相等的平行四边形是菱形，四边都相等的四边形是菱形。

2、性质：

(1)菱形的四条边都相等;

(2)菱形的对角线互相垂直，并且每一条对角线平分一组对角。

(3)菱形是轴对称图形，对称轴有2条，即两条对角线所在直线;

(4)菱形是中心对称图形;

(五)梯形

1、定义：一组对边平行而另一组对边不平行的四边形叫做梯形。平行的两边叫做梯形的底边，较长的一条底边叫下底，较短的一条底边叫上底。另外两边叫腰;夹在两底之间的垂线段叫梯形的高。

等腰梯形：两腰相等的梯形叫做等腰梯形。

2、性质：

(1)梯形的上下两底平行;

(2)梯形的中位线，平行于两底并且等于上下底和的一半;

(3)等腰梯形的对角线相等(可能垂直);

(4)等腰梯形是轴对称图形，它只有一条对称轴，一底的垂直平分线是它的对称轴。

以上就是关于四边形如何分类，如何区分四边形和平行四边形的全部内容，以及四边形如何分类的相关内容,希望能够帮到您。

版权声明：本文来自用户投稿，不代表【推酷网】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：350149276@qq.com）我们将及时处理，共同维护良好的网络创作环境。