红黑树原理是什么建立过程,红黑树之原理详解
发布:小编
本文目录
红黑树之原理详解
性质1: 每个节点要么是 黑色 ,要么是 红色 。
性质2: 根节点是 黑色 。
性质3: 每个叶子节点(NIL)是黑色。
性质4: 每个 红色 节点的两个子节点一定都是 黑色 。
性质5: 任意一个节点到每个叶子节点的路径都包含 数量相同 的 黑节点 。俗称: 黑高 !
从性质5又可以推出:
性质5.1: 如果一个节点存在黑子节点,那么该结点肯定有两个子节点。
插入操作包括两部分工作:
注意: 插入结点,必须为 红色 ,理由很简单,红色在父节点(如果存在)为黑色节点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。如果插入结点是黑色,那么插入位置所在的子树黑色结点总是1,必须做自平衡。
最简单的一种情景,直接把插入结点作为根结点就行
注意: 根据红黑树性质2: 根结点是黑色。还需要把插入结点设为黑色。
处理: 更新当前结点的值,为插入结点的值
由于插入的结点是红色的,当插入结点的父结点为黑色时,并不会影响红黑树的平衡,直接插入即可,无需做自平衡。
再次回想红黑树的性质2: 根结点是黑色。如果插入结点的父结点为 红结点 ,那么该父结点不可能为根结点,所以插入结点总是存在祖父结点。这一点很重要,因为后序的旋转操作肯定需要祖父结点的参与。
依据红黑树 性质4可知,红色结点不能相连===>祖父结点肯定为黑结点
因为不可以同时存在两个相连的红结点。那么此时该插入子树的红黑层数的情况是:黑红红。显然最简单的处理方式是把其改为: 红黑红
处理:
1.将P和U结点改为黑色
2.将PP改为红色
3.将PP设置为当前结点,进行后序处理
注意: 单纯从插入前来看,叔叔结点非红即空(NIL结点),否则的话破坏了红黑树性质5,此路径比其它路径多一个黑色结点。
处理:
处理:
该情景对应情景4.2,只是方向反转,直接看图
处理:
处理:
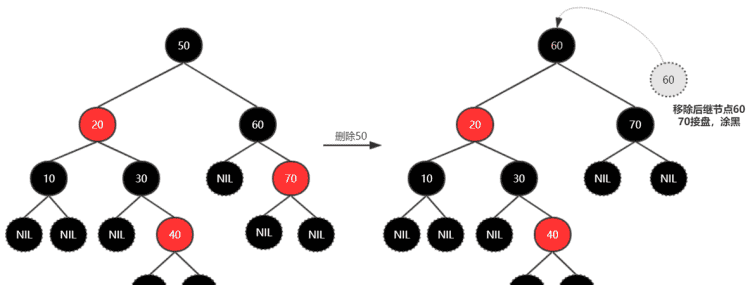
红黑树增加节点
在网上看了很多写红黑树的博客,大部分写的都不是很到位,有些关于红黑树的图都是有问题的,很多都没有说清楚什么情况促发哪种操作,看完之后还是不理解,在查看了很多资料之后,决定自己写关于红黑树的理解。分为添加节点篇和删除节点篇,本文为将阐述红黑树的基本原理以及在添加节点时,各种情况下对应的操作。(在看本文前,需要先了解平衡二叉树的原理,因为红黑树的有些操作和二叉平衡树类似)
红黑树之所以被称为红黑树,是因为红黑树的节点的颜色非红即黑,通过对节点颜色的限制和一系列的限制条件来确保红黑树没有任何一条路径是其他路径的两倍长。
红黑树需要满足以下条件:
(1)每个节点非黑即红。
(2)根节点是黑色。
(3)每个叶子节点,即空节点是黑的。
(4)红色节点的两个孩子节点都是黑的
(5)每个节点到子孙节点的所有路径上包含相同数量的黑色节点
如图1所示,就是一颗红黑树:
在插入节点时,总是插入红色节点,这样可以 尽量 避免破坏红黑树的结构,为什么说插入红节点可以 尽量 避免破坏红黑树的结构,假如现在要插入6,即插入到12节点的左孩子,如果6节点是黑色的,那么就会破坏规则(5),即图2中绿色路径上的黑色节点的数量比黄色路径上黑色节点的数量多,如果6节点是红色的,则不会破坏树结构,如图3所示。
红黑树节点的添加可分为以下3种情况
分析:因为插入的是红色节点,所以违背规则(2)根节点是黑色
解决方案:只需要把这个节点的颜色改成黑色即可。
分析:因为插入节点的颜色是红色,不会破坏任何规则。
解决方案:无。
分析:这时又可分为插入节点是父节点的左孩子还是右孩子,以及父节点是祖父节点的左孩子还是右孩子,由于对称性,我们只需要考虑其中一种即可。假设插入的节点是25,即如图4所示的位置。这时破坏了规则(4)红色节点的两个孩子节点都是黑的。
解决方案:将当前节点的父节点和叔叔节点改成黑色,祖父节点改为红色,把当前节点指向祖父节点。如图5所示。
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右孩子。
分析:这时破坏了规则(4)红色节点的两个孩子节点都是黑的。如图5所示。
解决方案:将当前节点的父节点作为新的当前节点,以新的当前节点为支点进行左旋。如图6所示。
[图片上传失败...(image-c45d5d-1594949705288)]
分析:这时破坏了规则(4)红色节点的两个孩子节点都是黑的。如图6所示。
解决方案:父节点改成黑色,祖父节点改成红色,将当前节点改为祖父节点,并以新的当前节点为支点进行右旋。如图7所示。
[图片上传失败...(image-492143-1594949705288)]
以上内容就是关于红黑树添加节点时的操作,本片博客参考了 ***/topics/350253651 。
红黑树——一个自平衡的二叉搜索树
普通的二叉搜索树在最坏的情况下,可能退化成一个链表。而又因为二叉搜索树的所有操作的性能(添加,删除,查找等),与二叉搜索树的高度有关。在最坏的情况下,二叉搜索树的高度和元素个数相同,此时二叉搜索树的效率降为了O(n)级别。
所以为了防止我们的二叉搜索树退化成一个链表,就产生了 平衡二叉树 。 平衡二叉树 可以保证它的左右两个子树的高度差不会超过1。平衡二叉树有很多实现,一个经典实现就是 红黑树 。
在红黑树中将树中的节点划分为两种状态,分别用黑色和红色来表示。
红黑树为了保证自己能够平衡子树,所以制订以下五个规则:
1、每个节点必须有颜色,要么黑色,要么红色,没有别的颜色。
2、根节点必须是黑色
3、所有的空节点(nil节点)都认为是黑色节点。
4、红色的节点不能连续,即一个红色的节点,它的父节点和子节点不能也是红色的,
5、无论从哪一个节点起始,到它每个叶子节点的路径中,黑色节点数量必须相同。
在对红黑树进行添加、删除等操作之后,必须使红黑树符合这5个规则。
那么问题来了,在添加删除操作之后,树中节点的数量都变了,是怎么保证整个树满足上述这些规则呢?
这里涉及到3种操作, 变色 、 左旋 和 右旋 。通过这个三种操作,在增删节点之后调整树的形状结构,使它满足上述5个规则。这也是红黑树能保持平衡的原因。
变色操作 我们在下文的添加、删除节点的实际操作中,再进行在描述。
先来说一下左右旋。
文字描述一下就是,2的右孩子节点4,变为了2的父节点,2由父节点变为4的左孩子。同时,4原来的左孩子变为2的右孩子。
右旋与左旋相反,即以某节点为支点进行顺时针旋转。同样,我们看下图,是以5为支点进行的右旋:
文字描述同样反过来,5的左孩子节点3,变为5的父节点,5由父节点变为3的右孩子。3原来的右孩子变为5的左孩子。
首先是在树中找到新节点正确的位置,寻找位置的过程与普通的二叉搜索树相同,只是将新插入的节点默认为 红色节点 。为什么默认为红色?因为如果你将新节点默认为黑色,则插入后肯定会打破原本符合规则的红黑树(上述第5条规则)。但是,如果你将新节点定为红色,则有可能不用任何操作就符合红黑树规则,如下图,当新插入的红色节点,它的父亲节点为黑色时候,此时已经满足红黑树规则了。所以用红色比黑色好。
如果很不巧,新插入的节点的父亲节点也为红色,因为红色节点不能连续,所以我们需要调整红黑树的结构使其满足规则。在调整的过程中我们会遇到3种需要处理的情况,我们来一一进行说明。
情况1:
插入新节点40, 此时它的父节点为红色,并且它的叔叔节点(即51)也为红色 。此时我们需要进行 变色 操作。 将该节点的父亲节点、叔叔节点都变为黑色,祖父节点变为红色 。
此时上图已经满足红黑树的规则。但有的时候我们经过了变色操作后,仍不满足红黑树的规则,会遇到下面的情况。
情况2:
如图,我们插入新的节点53,在按情况1的操作变色后,变成了这样:
最后我们说一下情况3的情景,如下图:
我们向树中插入新节点37,在按情况1的操作变色后,变成了这样:
情况3:
3种情况我们说明完了,但是你可能还会有这样的疑问,什么时候进行左旋,什么时候进行右旋;什么时候以父节点为支点旋转,什么时候又以祖父节点为支点旋转?
那么我们可以总结一下,当遇到连续的红色节点应该怎么办: 当前节点我们叫它X,如果X相对于父节点的左右位置和父节点相对于祖父节点的左右位置相同,此时,就以祖父节点为支点,进行反向旋转。例如:X为父节点的左孩子,X的父节点同样也是其祖父节点的左孩子,此时以祖父节点为支点进行右旋;
如果X相对于父节点的左右位置和父节点相对于祖父节点的左右位置不同,则以X的父节点为支点,进行旋转,旋转方向与X相对于父节点左右位置相反。例如:X为其父节点的左孩子,X的父节点为祖父节点的右孩子,此时以X的父节点为支点进行一次右旋。
在红黑树中删除节点,肯定要涉及到要删的这个节点是红色的还是黑色的。删除红色比较简单,我们先说一下删除红色节点。
删除节点要考虑这个节点所处的位置,所以我们罗列一下红色的节点所有可能的位置情况。
你可能会发现为什么少了一种情况?它不能只有左子树或者只有右子树吗?我们可以看下图:
很明显,这四种情况都不符合红黑树的规则,所以根本不会出现这种情况。
而对于既有左子树也有右子树的情况。 我们可以先和普通的二叉搜索树的删除操作一样,将它与前驱或者后继交换一下 。它就又变成第一种情况——成为了一个叶子节点。所以我们只需考虑当它是叶子节点的情况。
接下来我们看一下当要删除的节点是黑色的时候应该怎么办。
同样我们列一下节点位置可能的情况:
第三种情况和删除红色节点时的处理方法一样,可以转换成第一种或第二种情况,所以我们只关心前两种情况。
当要删除的黑色节点只有一个子树时:
最后我们看一下最难处理的一种情况。
要删除的黑色节点是叶子节点时:
情况1:待删除黑色节点20,它的兄弟节点为红色。
操作方法为:将远侄子节点变黑,兄弟节点与父亲节点互换颜色,最后以父节点为支点进行 左旋 。(为什么是左旋?因为待删除的20是左孩子,我们要将左子树长度拉长,将它沉下来,使它变成多余的节点好删除它,如果它是右孩子,则进行右旋)
操作后如下图就完成了。
情况3:待删除黑色节点20,它的兄弟节点为黑色,但它没有红色的远侄子节点(即nil点,记住,nil点算黑色),只有红色的近侄子节点。
操作后如下图:
此时有了红色的远侄子,就满足了情况2,再按情况2进行一次操作就完成了。
情况4:待删除黑色节点20,它的兄弟节点为黑色,远侄子、近侄子节点都没有。(即两个nil节点,nil节点算黑色)
我们将上图红黑树按流程演示一下:
第一步按情况4操作,将55变红。并将父节点50看做当前节点,继续操作。
此时有关红黑树的知识就说完了。
以上所有内容都为自己查阅资料学习理解之后手敲的。尽量得采用通俗易懂的描述和解释让读者更明白。27张图都是自己亲自画的,花费了四天才写完,如果觉得写的还可以,麻烦点亮喜欢支持一下,如果还是不懂,可以下方留言QQ等联系方式,我亲自告诉你。
红黑树时间复杂度 平均时间复杂度
红黑树性质与时间复杂度证明扩展:
一、红黑树性质:
1.结点必须是红色或者黑色。
2.根节点必须是黑色。
3.叶节点(NIL)必须是黑色(NIL节点无数据,是空节点)。
4.如果一个节点是红色的,则它的子节点必须是黑色的。
5.从任一节点出发到其每个叶子节点的路径,黑色节点的数量必须相等。
二、时间复杂度证明:
首先我们要知道O(logn)中的n是指红黑树节点个数。
已知一条关于红黑树的定理:一棵有n个节点的红黑树高度h至多为2log(n+1)。(h<=2log(n+1))只要证明这条定理成立,时间复杂度也就成立的(因为红黑树查询的时间复杂度其实就是从根节点开始往下查询,最大查询时叶节点终止,即为树的高度),接下来就来证明这条定理。
推理过程:
1、h<=2log(n+1)可推出n>=2^(h/2)-1。得出定理的逆否命题是"高度为h的红黑树,它包含的节点个数至少为2^(h/2)-1个,需证明逆否命题为真,即证明了原命题为真。
2、从某个节点x出发(不包括该节点)到达一个叶节点的任意一条路径上,黑色节点的个数称为该节点的黑高度(x'sblackhe为bh(x)。
3、根据性质五可知,从节点x出发到达所有的叶节点都具有相同数目的黑节点。这也就意味着,bh(x)的值是唯一的!
以上就是关于红黑树原理是什么建立过程,红黑树之原理详解的全部内容,以及红黑树的原理的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。

