邻角互补是什么意思,邻补角的定义是什么意思
发布:小编
本文目录
邻补角的定义是什么意思
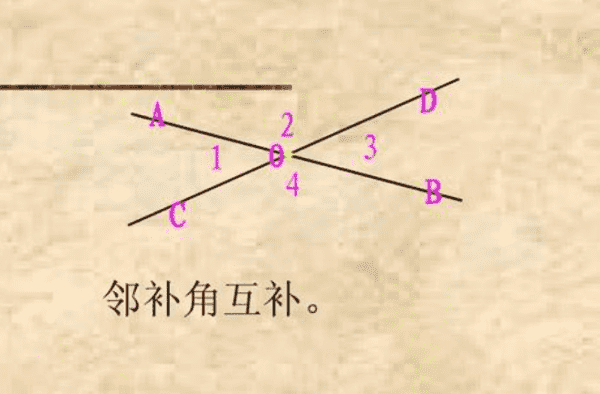
两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角。
注:补角只注重数量关系两角之和是180°,即无论是否有公共边均可,但邻补角还要注重位置上的关系。一个角与它的邻补角的和等于180°。如果两个角互为邻补角,那么它们的角平分线互相垂直。
扩展资料
补角与余角的区别:
1、定义不同:
如果两个角的和是一个平角,那么这两个角互为补角,其中一个角叫做另一个角的补角 。
∠A +∠C=180°即:∠C的补角=180°-∠C; ∠A的补角=180°-∠A
如果两个角的和是一个直角,那么称这两个角互为余角,简称互余。其中一个角是另一个角的余角。
∠A +∠C=90°即:∠C的余角=90°-∠C ;∠A的余角=90°-∠A
2、计算方法不同:
补角:180度减去这个角的度数。
余角:90度减去这个角的度数。
余角必由两个锐角组成,互补的两角,必有其一为钝角或直角。
邻补角的定义是什么意思
邻补角的定义为:“若两个角有一条公共边以及共同的顶点,那么这两个角被称作一对邻补角,也可以将其中的一个角称为另一个角的邻补角”。
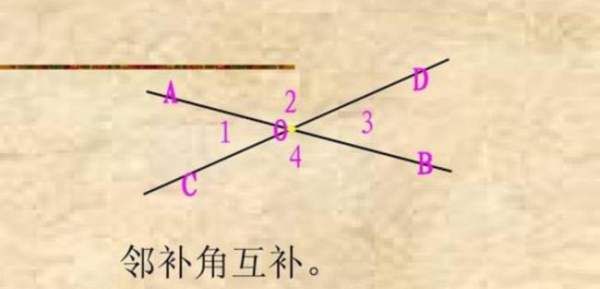
如下图中的,∠AOC有两个邻补角,分别是∠AOD和∠COB。形如此种类型的角,就叫做邻补角,邻补角最明显的特征是相邻着且角度之和为180°,这是判断的重要方法。
扩展资料:
邻补角的两个重要性质:一个角与它的邻补角的和等于180°、如果两个角互为邻补角,那么它们的角平分线互相垂直。
邻补角的特征识别:
1、具有一个公共的顶点、有一条公共边、两个角的另一边互为反向延长线、邻补角是成对出现的,而且是互为邻补角。
2、互为邻补角的两角相拼为平角、互为邻补角的两角互补,即相加为180度。
邻补角包括两个方面的要求:两角的位置关系、数量关系。补角,指的是数量关系满足两角之和等于180度、邻角,指的是位置关系满足两角有公共的顶点和公共的边。
邻补角是一种特殊的互补角。邻补角的两条非公共边构成一条直线。
对角线互相平分的平行四边形是什么形
对角线互相平分:平行四边形有两条对角线,相交点把各自分成两段,各自的两段长是相等的。换句话,一条对角线从另一条对角线的中心点穿过,将另一条对角线分成长度相等的两段。
邻角互补,就是任意相邻的两个角的和是180度。
邻补角是什么意思
邻补角是指两个相邻的补角,即互为相邻角度和为180度的角。补角是指两个角度的和等于180度的角对。
具体而言,如果有一个角A和它旁边的角B,且角A和角B的和等于180度,则这两个角就是邻补角。邻补角可以是相邻的内角或者相邻的外角,只要它们的和为180度即可。
在几何中,邻补角具有一些特殊的性质。例如,邻补角的补角是相等的,即如果角A和角B是邻补角,那么它们各自的补角也是相等的。此外,邻补角的和总是等于180度,无论角度的大小如何变化。

拓展资料:
邻补角在解决几何问题和证明几何定理时经常会被应用到,通过研究和利用邻补角的性质,可以帮助我们更好地理解和推导几何关系。
邻补角是几何学中一个重要的概念,它在解决角度相关问题和证明几何定理时具有广泛的应用。通过深入了解邻补角的性质和特点,我们可以更好地运用它们来推导和解决几何难题。
首先,邻补角的定义是两个相邻的角度和为180度。这意味着当我们遇到一道题目,已知两个角度互为补角,并且它们是相邻的,我们可以得出它们的和为180度。利用这个性质,我们可以根据已知条件来解决问题,找出所需的未知角度或构造几何图形。
其次,邻补角还具有一些重要的性质。首先,邻补角的补角是相等的。也就是说,如果角A和角B是邻补角,那么它们各自的补角也是相等的。这个性质可以直接应用在计算角度大小或者证明两个角度相等的问题中。
此外,邻补角的和总是等于180度。无论角度的大小如何变化,只要它们是邻补角关系,它们的和都将保持不变。这一点在解决复杂几何问题中尤为有用,通过利用邻补角的和为180度的性质,我们可以简化计算或者推导出其他角度的关系。

需要注意的是:
邻补角的概念不仅适用于相邻的内角,还适用于相邻的外角。只要两个角度满足和为180度的条件,它们就可以被称为邻补角。这使得邻补角的应用范围更加广泛,可以覆盖更多的几何问题。
总之,邻补角作为几何学中一个重要的概念,在解决几何难题和证明几何定理时具有重要的作用。通过研究和利用邻补角的性质,我们可以更好地理解和推导几何关系,从而提高解题的准确性和效率。
以上就是关于邻角互补是什么意思,邻补角的定义是什么意思的全部内容,以及邻角互补是什么意思的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。

