双曲线的焦距是什么，双曲线焦点到顶点的距离公式

双曲线的焦距是什么

一般来说，双曲线的焦距是双曲线的两个焦点之间的距离，焦距=2c，双曲线的焦距公式为c=√(a^2+b^2)。“椭圆焦距的意思：椭圆两个焦点间的距离，椭圆焦距的计算公式：焦距=2c。

一般的，双曲线（希腊语“περβολ”，字面意思是“超过”或“超出”）是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

它还可以定义为与两个固定的点（叫做焦点）的距离差是常数的点的轨迹。这个固定的距离差是a的两倍，这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的实半轴。焦点位于贯穿轴上，它们的中间点叫做中心，中心一般位于原点处。

在数学中，双曲线（多重双曲线或双曲线）是位于平面中的一种平滑曲线，由其几何特性或其解决方案组合的方程定义。双曲线有两片，称为连接的组件或分支，它们是彼此的镜像，类似于两个无限弓。

双曲线是由平面和双锥相交形成的三种圆锥截面之一。（其他圆锥部分是抛物线和椭圆，圆是椭圆的特殊情况）如果平面与双锥的两半相交，但不通过锥体的顶点，则圆锥曲线是双曲线。

双曲线焦点到顶点的距离公式

双曲线的第一定义是:动点到两定点距离差的绝对值等于定长的轨迹称为双曲线.

其中两定点间距离称为焦距,(设为2c),距离差称为长轴长(记为2a),

设b^2=c^2-a^2,称2b为虚轴长.其中a称为半长轴长,b称为半虚轴长.

a有几何意义,中心到顶点的距离.b也有几何意义,以中心为原点,以坐标轴为对称轴的双曲线,过点(a,b)和(-a,-b),(a,-b)和(-a,b)的两条直线是这双曲线的渐近线.

单纯讲半长轴,半虚轴是不够恰当的.

双曲线的焦距计算公式

B

试题分析：∵

，∴

，∴双曲线

的焦距为2c=

，故选C。

点评：双曲线的性质在高考中通常以选择题形式出现，难度不大，要求学生掌握最基本的知识。

双曲线的焦距怎么算出来的

在X轴上的是(c,0)和(-c,0)

在Y轴的是（0，c)和(0，-c)

c=根号(a^2+b^2)

我们把平面内与两个定点F1，F2的距离的差的绝对值等于一个常数（常数为2a，小于|F1F2|）的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线）

即：│|PF1|-|PF2│|=2a

定义1：

平面内，到两个定点的距离之差的绝对值为常数（小于这两个定点间的距离）的点的轨迹称为双曲线。定点叫双曲线的焦点。

定义2：平面内，到给定一点及一直线的距离之比为常数e（（e>1），即为双曲线的离心率）的点的轨迹称为双曲线。定点叫双曲线的焦点，定直线叫双曲线的准线。双曲线准线的方程为（焦点在x轴上）或（焦点在y轴上）。

定义3：一平面截一圆锥面，当截面与圆锥面的母线不平行也不通过圆锥面顶点，且与圆锥面的两个圆锥都相交时，交线称为双曲线。

定义4：在平面直角坐标系中，二元二次方程F（x，y）=ax2+bxy+cy2+dx+ey+f=0满足以下条件时，其图像为双曲线。

1、a、b、c不都是零。

2、Δ=b2-4ac>0。

注：第2条可以推出第1条。

在高中的解析几何中，学到的是双曲线的中心在原点，图像关于x，y轴对称的情形。

上述的四个定义是等价的，并且根据建好的前后位置判断图像关于x，y轴对称。

标准方程为：

1、焦点在X轴上时为：

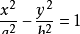
（a>0，b>0）

2、焦点在Y轴上时为：

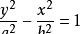
（a>0，b>0）

扩展资料：

取值范围

│x│≥a（焦点在x轴上）或者│y│≥a（焦点在y轴上）。

对称性

关于坐标轴和原点对称，其中关于原点成中心对称。

顶点

A（-a，0），A'（a，0）。同时AA'叫做双曲线的实轴且│AA'│=2a。

B（0，-b），B'（0，b）。同时BB'叫做双曲线的虚轴且│BB'│=2b。

F1（-c，0）或（0，-c），F2（c，0）或（0，c）。F1为双曲线的左焦点，F2为双曲线的右焦点且│F1F2│=2c

对实轴、虚轴、焦点有：a2+b2=c2

渐近线

焦点在x轴：

。

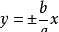
焦点在y轴：

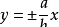
圆锥曲线ρ=ε/1-ecosθ当e>1时，表示双曲线。其中p为焦点到准线距离，θ为弦与x轴夹角。

令1-ecosθ=0可以求出θ，这个就是渐近线的倾角，即θ=arccos（1/e）

令θ=0，得出ρ=ε/（1-e），x=ρcosθ=ε/（1-e）

令θ=π，得出ρ=ε/（1+e），x=ρcosθ=-ε/（1+e）

这两个x是双曲线定点的横坐标。

求出它们的中点的横坐标（双曲线中心横坐标）

x=[（ε/1-e）+（-ε/1+e）]/2

（注意化简一下）

直线ρcosθ=[（ε/1-e）+（-ε/1+e）]/2

是双曲线一条对称轴，注意是不与曲线相交的对称轴。

将这条直线顺时针旋转π/2-arccos（1/e）角度后就得到渐近线方程，设旋转后的角度是θ’

则θ’=θ-[π/2-arccos（1/e）]

则θ=θ’+[π/2-arccos（1/e）]

代入上式：

ρcos{θ’+[π/2-arccos（1/e）]}=[（ε/1-e）+（-ε/1+e）]/2

即：ρsin[arccos（1/e）-θ’]=[（ε/1-e）+（-ε/1+e）]/2

然后可以用θ取代式中的θ’了

得到方程：ρsin[arccos（1/e）-θ]=[（ε/1-e）+（-ε/1+e）]/2

现证明双曲线x2/a2-y2/b2=1上的点在渐近线中

设M（x，y）是双曲线在第一象限的点，则

y=（b/a）√（x2-a2）（x>a）

因为x2-a2

即y

所以，双曲线在第一象限内的点都在直线y=bx/a下方。

根据对称性第二、三、四象限亦如此。

参考资料：

以上就是关于双曲线的焦距是什么，双曲线焦点到顶点的距离公式的全部内容，以及双曲线的焦距是什么的相关内容,希望能够帮到您。

版权声明：本文来自用户投稿，不代表【推酷网】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：350149276@qq.com）我们将及时处理，共同维护良好的网络创作环境。