函数连续的充要条件,函数连续的条件

本文目录

• 1.函数连续的条件
• 2.函数连续的充要条件是什么
• 3.连续的充要条件是什么
• 4.函数连续的充要条件

函数连续的条件

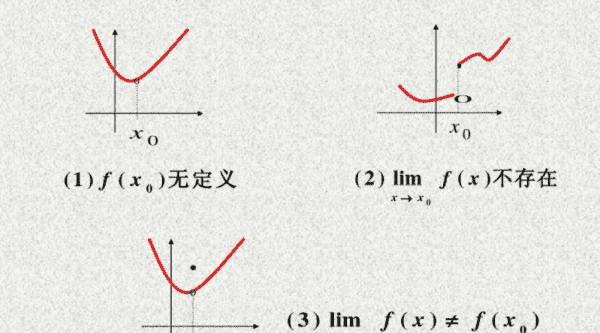
1、充分条件：若函数f（x）在x0可导或可微（或者更强的条件），则函数在x0连续。

2、必要条件：若函数f（x）在x0无定义、或无极限、或极限不等于函数值，则在x0不连续。

3、若函数f（x）在x0有定义，且极限与函数值相等。则函数在x0连续。

4、连续函数的法则：定理一：在某点连续的有限个函数经有限次和、差、积、商（分母不为0） 运算，结果仍是一个在该点连续的函数。定理二：连续单调递增 （递减）函数的反函数，也连续单调递增 （递减）。定理三：连续函数的复合函数是连续的。

函数连续的充要条件是什么

解：

x→0＋

lim｜sinx｜＝limsinx＝0＝sin0

x→0－

limsinx＝lim－sinx＝0＝sin0

左右都连续．所以连续

x→0＋

lim（｜sinx｜－｜sin0）｜／（x－0）＝limsinx／x＝1

x→0－

lim（｜sinx｜－｜sin0）｜／（x－0）＝lim－sinx／x＝－1

左右导数不等，所以不可导。

连续性：y在X的领域内处有定义，而且y在X趋向于0时极限存在，而且极限值等于y在X＝0的值。证明极限存在，要看左右极限是否存在且相等，像这函数，左右极限都存在，且都等于0，而且极限值等于函数值。

可导性：先对函数进行求导，再求其在X＝0处左右极限是否存在且相等，如果不存在，则不可导，如果存在可是不相等，也不可导。

扩展资料

函数的连续性：

在定义函数的连续性之前先了解一个概念——增量设变量x从它的一个初值x1变到终值x2，终值与初值的差x2－x1就叫做变量x的增量，记为：△x即：△x＝x2－x1增量△x可正可负。

设函数在区间［a，b）内有定义，如果右极限存在且等于，即：＝，那么就称函数在点a右连续。一个函数在开区间（a，b）内每点连续。

则为在（a，b）连续，若又在a点右连续，b点左连续，则在闭区间［a，b］连续，如果在整个定义域内连续，则称为连续函数。

注：一个函数若在定义域内某一点左、右都连续，则称函数在此点连续，否则在此点不连续。注：连续函数图形是一条连续而不间断的曲线。

连续的充要条件是什么

判断函数f(x)在x0点处连续，当且仅当f(x)满足以下三个充要条件：

1、f(x)在x0及其左右近旁有概念。

2、f(x)在x0的极限存在。

3、f(x)在x0的极限值与函数值f(x0)相等。

简介

所有多项式函数都是连续的。各类初等函数，如指数函数、对数函数、平方根函数与三角函数在它们的定义域上也是连续的函数。

绝对值函数也是连续的。定义在非零实数上的倒数函数f= 1/x是连续的。但是如果函数的定义域扩张到全体实数，那么无论函数在零点取任何值，扩张后的函数都不是连续的。

函数连续的充要条件

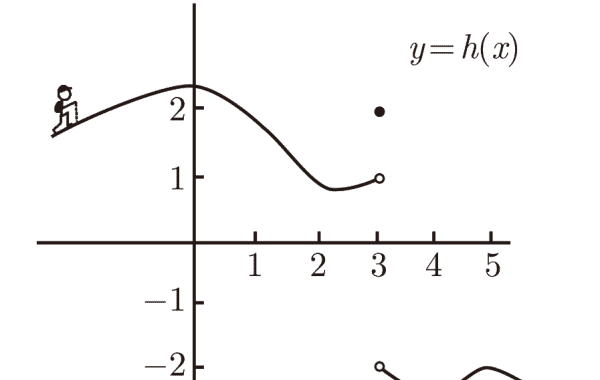
函数在某点可导的充要条件是函数在该点的左右极限都存在且相等。 也可以说是左导数和右导数都存在且相等。

左极限就是函数从一个点的左侧无限靠近该点时所取到的极限值，且误差可以小到我们任意指定的程度，只需要变量从坐标充分靠近于该点。

右极限就是函数从一个点的右侧无限靠近该点时所取到的极限值，且误差可以小到我们任意指定的程度，只需要变量从坐标充分靠近于该点。

扩展资料

所有多项式函数都是连续的。各类初等函数，如指数函数、对数函数、平方根函数与三角函数在它们的定义域上也是连续的函数。

绝对值函数也是连续的。

定义在非零实数上的倒数函数f= 1/x是连续的。但是如果函数的定义域扩张到全体实数，那么无论函数在零点取任何值，扩张后的函数都不是连续的。

非连续函数的一个例子是分段定义的函数。例如定义f为：f(x) = 1如果x> 0，f(x) = 0如果x≤ 0。取ε = 1/2，不存在x=0的δ-邻域使所有f(x)的值在f(0)的ε邻域内。直觉上我们可以将这种不连续点看做函数值的突然跳跃。

以上就是关于函数连续的充要条件,函数连续的条件的全部内容，以及函数连续的充要条件的相关内容,希望能够帮到您。

版权声明：本文来自用户投稿，不代表【推酷网】立场，本平台所发表的文章、图片属于原权利人所有，因客观原因，或会存在不当使用的情况，非恶意侵犯原权利人相关权益，敬请相关权利人谅解并与我们联系（邮箱：350149276@qq.com）我们将及时处理，共同维护良好的网络创作环境。