如何解答数量关系题,两数之差是什么意思
发布:小编
本文目录
两数之差是什么意思
鸡兔同笼中的总头数是“两数之和”,如果把条件换成“两数之差”,又应该怎样去解呢?
例7 买一些4分和8分的邮票,共花6元8角.已知8分的邮票比4分的邮票多40张,那么两种邮票各买了多少张?
解一:如果拿出40张8分的邮票,余下的邮票中8分与4分的张数就一样多.
(680-8×40)÷(8+4)=30(张),这就知道,余下的邮票中,8分和4分的各有30张.
因此8分邮票有40+30=70(张).
答:买了8分的邮票70张,4分的邮票30张.
也可以用任意假设一个数的办法.
解二:譬如,假设有20张4分,根据条件“8分比4分多40张”,那么应有60张8分.以“分”作为计算单位,此时邮票总值是4×20+8×60=560.比680少,因此还要增加邮票.为了保持“差”是40,每增加1张4分,就要增加1张8分,每种要增加的张数是:
(680-4×20-8×60)÷(4+8)=10(张).
因此4分有20+10=30(张),8分有60+10=70(张).
例8 一项工程,如果全是晴天,15天可以完成.倘若下雨,雨天一天工程要多少天才能完成?
解:类似于例3,我们设工程的全部工作量是150份,晴天每天完成10份,雨天每天完成8份.用上一例题解一的方法,晴天有
(150-8×3)÷(10+8)= 7(天).
雨天是7+3=10天,总共7+10=17(天).
答:这项工程17天完成.
请注意,如果把“雨天比晴天多3天”去掉,而换成已知工程是17天完成,由此又回到上一节的问题.差是3,与和是17,知道其一,就能推算出另一个.这说明了例7、例8与上一节基本问题之间的关系.[NextPage]
总脚数是“两数之和”,如果把条件换成“两数之差”,又应该怎样去解呢?
例9 鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只?
解一:假如再补上28只鸡脚,也就是再有鸡28÷2=14(只),鸡与兔脚数就相等,兔的脚是鸡的脚4÷2=2(倍),于是鸡的只数是兔的只数的2倍.
兔的只数是:(100+28÷2)÷(2+1)=38(只).
鸡是:100-38=62(只).
答:鸡62只,兔38只.
当然也可以去掉兔28÷4=7(只).兔的只数是(100-28÷4)÷(2+1)+7=38(只).
也可以用任意假设一个数的办法.
解二:假设有50只鸡,就有兔100-50=50(只).此时脚数之差是:
4×50-2×50=100,
比28多了72.就说明假设的兔数多了(鸡数少了).为了保持总数是100,一只兔换成一只鸡,少了4只兔脚,多了2只鸡脚,相差为6只(千万注意,不是2).因此要减少的兔数是:
(100-28)÷(4+2)=12(只).
兔只数是:
50-12=38(只).
另外,还存在下面这样的问题:总头数换成“两数之差”,总脚数也换成“两数之差”.
例10 古诗中,五言绝句是四句诗,每句都是五个字;七言绝句是四句诗,每句都是七个字.有一诗选集,其中五言绝句比七言绝句多13首,总字数却反而少了20个字.问两种诗各多少首.
解一:如果去掉13首五言绝句,两种诗首数就相等,此时字数相差
13×5×4+20=280(字).
每首字数相差:7×4-5×4=8(字).
因此,七言绝句有:28÷(28-20)=35(首).
五言绝句有:35+13=48(首).
答:五言绝句48首,七言绝句35首.[NextPage]
解二:假设五言绝句是23首,那么根据相差13首,七言绝句是10首.字数分别是20×23=460(字),28×10=280(字),五言绝句的字数,反而多了:460-280=180(字).与题目中“少20字”相差:180+20=200(字).
说明假设诗的首数少了.为了保持相差13首,增加一首五言绝句,也要增一首七言绝句,而字数相差增加8.因此五言绝句的首数要比假设增加
200÷8=25(首).
五言绝句有
23+25=48(首).
七言绝句有
10+25=35(首).
在写出“鸡兔同笼”公式的时候,我们假设都是兔,或者都是鸡,对于例7、例9和例10三个问题,当然也可以这样假设.现在来具体做一下,把列出的计算式子与“鸡兔同笼”公式对照一下,就会发现非常有趣的事.
例7,假设都是8分邮票,4分邮票张数是(680-8×40)÷(8+4)=30(张).
例9,假设都是兔,鸡的只数是(100×4-28)÷(4+2)=62(只).
例10,假设都是五言绝句,七言绝句的首数是(20×13+20)÷(28-20)=35(首).
首先,请读者先弄明白上面三个算式的由来,然后与“鸡兔同笼”公式比较,这三个算式只是有一处“-”成了“+”.其奥妙何在呢?当你进入初中,有了负数的概念,并会列二元一次方程组,就会明白,从数学上说,这一讲前两节列举的所有例子都是同一件事.
例11
有一辆货车运输2000只玻璃瓶,运费按到达时完好的瓶子数目计算,每只2角,如有破损,破损瓶子不给运费,还要每只赔偿1元.结果得到运费379.6元,问这次搬运中玻璃瓶破损了几只?
解:如果没有破损,运费应是400元.但破损一只要减少1+0.2=1.2(元).因此破损只数是(400-379.6)÷(1+0.2)=17(只).
答:这次搬运中破损了17只玻璃瓶.
请你想一想,这是“鸡兔同笼”同一类型的问题吗?
例12 有两次自然测验,第一次24道题,答对1题得5分,答错(包含不答)1题倒扣1分;第二次15道题,答对1题8分,答错或不答1题倒扣2分,小明两次测验共答对30道题,但第一次测验得分比第二次测验得分多10分,问小明两次测验各得多少分?
解一:如果小明第一次测验24题全对,得5×24=120(分).那么第二次只做对30-24=6(题)得分是:8×6-2×(15-6)=30(分). 两次相差:120-30=90(分).
比题目中条件相差10分,多了80分.说明假设的第一次答对题数多了,要减少.第一次答对减少一题,少得5+1=6(分),而第二次答对增加一题不但不倒扣2分,还可得8分,因此增加8+2=10分.两者两差数就可减少6+10=16(分).(90-10)÷(6+10)=5(题).
因此,第一次答对题数要比假设(全对)减少5题,也就是第一次答对19题,第二次答对:30-19=11(题).
第一次得分:5×19-1×(24- 9)=90.
第二次得分:8×11-2×(15-11)=80.
答:第一次得90分,第二次得80分.[NextPage]
解二:答对30题,也就是两次共答错
24+15-30=9(题).
第一次答错一题,要从满分中扣去5+1=6(分),第二次答错一题,要从满分中扣去8+2=10(分).答错题互换一下,两次得分要相差6+10=16(分).
如果答错9题都是第一次,要从满分中扣去6×9.但两次满分都是120分.比题目中条件“第一次得分多10分”,要少了6×9+10.因此,第二次答错题数是:(6×9+10)÷(6+10)=4(题)·
第一次答错 9-4=5(题).
第一次得分 5×(24-5)-1×5=90(分).
第二次得分 8×(15-4)-2×4=80(分).
习题二
1.买语文书30本,数学书24本共花83.4元.每本语文书比每本数学书贵0.44元.每本语文书和数学书的价格各是多少?
2.甲茶叶每千克132元,乙茶叶每千克96元,共买这两种茶叶12千克.甲茶叶所花的钱比乙茶叶所花钱少354元.问每种茶叶各买多少千克?
3.一辆卡车运矿石,晴天每天可运16次,雨天每天只能运11次.一连运了若干天,有晴天,也有雨天.其中雨天比晴天多3天,但运的次数却比晴天运的次数少27次.问一连运了多少天?
4.某次数学测验共20道题,做对一题得5分,做错一题倒扣1分,不做得0分.小华得了76分.问小华做对了几道题?
5.甲、乙二人射击,若命中,甲得4分,乙得5分;若不中,甲失2分,乙失3分.每人各射10发,共命中14发.结算分数时,甲比乙多10分.问甲、乙各中几发?
6.甲、乙两地相距12千米.小张从甲地到乙地,在停留半小时后,又从乙地返回甲地,小王从乙地到甲地,在甲地停留40分钟后,又从甲地返回乙地.已知两人同时分别从甲、乙两地出发,经过4小时后,他们在返回的途中相遇.如果小张速度比小王速度每小时多走1.5千米,求两人的速度.

数量关系猜题技巧中公
数量关系板块让绝大部分同学感到头疼,这个版块考场上98%的考生是连蒙带猜完成的,如果靠蒙,也要讲究方法和战术,“微行测”总结了近几年数量关系考试真题,特总结了五大实用的猜题技巧:
技巧一:观察题干,如果题目中存在比例关系,在选项中选择满足该比例中数字整除特性的选项为正解。
【例题】某城市共有四个区,甲区人口数是全城的4/13,乙区的人口数是甲区的5/6,丙区人口数是前两区人口数的4/11,丁区比丙区多4000人,全城共有人口多少万?
A.18.6万 B.15.6万 C.21.8万 D.22.3万
【点拨】这种题不需要直接计算,可以用“数字特征法”快速得出答案。看到“甲区人口数是全城的4/13”这句话,可以知道全程总人数应该是13的倍数,四个选项中只有B符合要求。
技巧二:对于最值问题,四个选项同增或同减,不论是最大还是最小,答案基本都在B、C项。
【例题】一环形跑道上画了100个标记点,已知相邻任意两个标记点之间的跑道距离相等。某人在环形跑道上跑了半圈,问他最多能经过几个标记点?
A.49 B.51 C.50 D.100
【点拨】问题为他最多能经过几个标记点,四个选项依次增大,根据我们的猜题经验,答案在B、C选项中。
对于最值问题,不论是国考还是省考,每年最少都有两道题,属于高频考题。通过对近几年的真题答案的梳理,该方法猜题正确率高达95%。
技巧三:通过对重庆2011下 — 2016上行测真题答案的总结:历年来第一道题不选D、第六道题不选A;三个连号题目及以上从未出现过相同的选项, 比如31、32、33,从未出现A、A、A;四个连号题目从未出现过A、B、C、D,比如51、52、53、54这4题的选项尽千万不要猜成:ABCD!
技巧四:通过对重庆2011下-2016上数量关系90道题目的统计,我们发现数量关系最多数情况是选C,占总数的30%;其次是选B,占总数的26%。如果在考场上,如果大家能确切做出1-2题,比如选的B项,剩下的题目建议都选C。
技巧五:通过大量数量关系试题验证:难题的答案放前边,易题的答案放后边 。换句话说,难题的答案在AB,易题的答案在CD。AB又如何确定到底选哪一个呢?通常来说,读完题目,明显感到题目非常绕,无从下手的答案在A。易题中CD又如何抉择呢?通常来说,估计多数人都做得起的题答案在D,估计多数人都做得起但要花较多时间的答案在C。
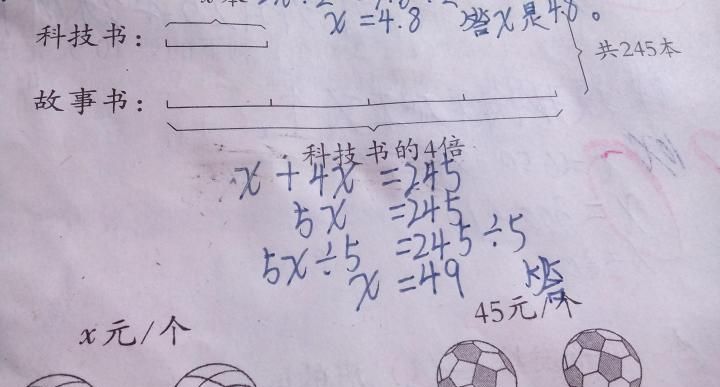
如何快速解答数量关系
1、特值法
2、分合法
3、比列法
4、尾数计算法
经验步骤:
1特值法,就是在某一范围内取一个特殊值,将复杂问题简单化,其中设“1”是最常用的特值法。
2分合法,这个主要适用于分类讨论和分步讨论题,主要是排列组合题。遇到多种情况加以分类,并逐步求解,然后再综合。而分步讨论法是分成几步,然后一步一步的解决。
3比列法,根据题干数据,解题画图,将各个份数画出来,进行分析,能简化难题,加速解题。
4尾数计算法,这是一个非常重要的方法,当四个答案全部相同时,可以采用尾数计算法,最后得出正确答案。
更多关于如何解答数量关系题,进入:
查看更多内容

数学跑道中的追及问题
一、环形相遇
甲和乙如果从同一点出发,反向而行,那么他们两个终会相遇,从开始到第一次相遇时,二者的路程和是1圈,从开始到第二次相遇,二者的路程和是2圈……从开始到第n次相遇,二者的路程和是n圈。假设1圈的长度为S,

这是基本公式,接下来我们通过例题来体现基本公式的应用。
例1:有一条400米长的环形跑道,甲、乙两人骑车从A点出发,背向而行。甲的初始速度为l米/秒,乙的初始速度为11米/秒。每当两人相遇,甲的速度就增加l米/秒,乙的速度减少l米/秒。那么当两人以相等的速度相遇时,距离A点多少米?
A.50 B.60 C.75 D.100
【答案】D。
【中公解析】二者第一次相遇的速度和为1+11=12,第二次相遇的速度和为2+10=12,第三次相遇的速度和为3+9=12,第四次相遇的速度和为4+8=12,第五次相遇的速度和为5+7=12,第六次相遇的速度和为6+6=12。虽然二者的速度不断发生变化,但速度和并没有发生改变,每次相遇的时间都是400÷12。甲走过的总路成为400÷12×(1+2+3+4+5+6)=700,也就是1圈多出300米。离起初的A点相距100米,故选D。
例2:甲、乙两人从运动场同一起点同向出发,甲跑步的速度为200米/分钟,乙步行,当甲第五次超越乙时,乙正好走完第三圈,再过1分钟,甲在乙前方多少米?
A.105 B.115 C.120 D.125
【答案】D。
【中公解析】当甲第5次超越乙时,路程差就是5圈。乙正好走完第3圈,则甲正好跑完8圈。同样的时间里,甲乙的路程之比是8:3,则二者的速度之比也是8:3,甲的速度为200,则乙的速度为75。所以1分钟后,甲在乙前方(200-75)×1=125米。故选D。
环形相遇和追及的题目难度并不比直线相遇和追及的难度大,甚至还会更简单。所以云南中公教育专家提醒大家千万不要自己吓唬自己。
以上就是关于如何解答数量关系题,两数之差是什么意思的全部内容,以及如何解答数量关系题的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。
大家都在看
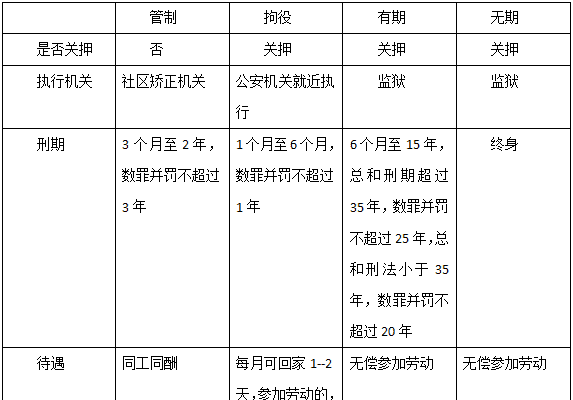
犯罪预备的处罚原则有哪些,根据刑法的规定为了犯罪什么是犯罪预备多选题
综合百科本文目录1.根据刑法的规定为了犯罪什么是犯罪预备多选题2.犯罪预备会减轻处罚吗3.对于预备犯的处罚原则4.违法预备行为如何处理根据刑法的规定为了犯罪什么是犯罪预备多选题法律主观:属于,犯罪预备是指为了犯罪而准备工具、制造条件。 刑罚 的本质目的在于通过对犯罪行为实施者的惩罚,起到

什么是光刻机
综合百科什么是光刻机光刻机又名:掩模对准曝光机,曝光系统,光刻系统等。常用的光刻机是掩膜对准光刻,所以叫MaskAlignmentSystem。一般的光刻工艺要经历硅片表面清洗烘干、涂底、旋涂光刻胶、软烘、对准曝光、后烘、显影、硬烘、刻蚀等工序。Photolithography(光刻)意

关于肚子饿的搞笑句子,怎么形容肚子饿发出的声音
综合百科本文目录1.怎么形容肚子饿发出的声音2.形容肚子饿的幽默句子搞笑3.形容肚子饿的幽默句子搞笑4.肚子饿的搞笑说说心情短语怎么形容肚子饿发出的声音1、冬天,早上不要总是呆在床上。记得吃早餐,喝一些热牛奶和吃一些热的食物,否则你会饿和冷。少吃面包和零食。2、苦藤老树昏鸦,饭堂里又出了

怎么测单反坏点,如何测试数码单反相机的坏点呢
综合百科怎么测单反坏点测试单反坏点步骤如下:用一黑色的纸张盖住镜头,单反相机选择手动模式,按下一次到两次快门,然后取出相片放进电脑,用电脑图片查看器打开图片放大到100%。看完整张相片是否有亮点。单镜头反光式取景照相机,(SingleLensReflexCamera,缩写为SLRcame

数码相机和单反相机有什么区别
综合百科数码相机和单反相机有什么区别普通数码相机中最快快门速度最大只能维持在1/1000秒左右;而单反数码相机轻松就能达到1/10000秒左右。数码相机对抖动是很敏感的,在曝光过程中即便轻微晃动,都会产生模糊的照片。而单反数码相机则可以外加镜头来防止抖动。数码相机,英文全称:Digita

在水下可以睁开眼睛,在水下不戴泳镜可以睁开眼睛游泳
综合百科本文目录1.在水下不戴泳镜可以睁开眼睛游泳吗2.人在水下能睁眼睛吗3.人在海里可以睁开眼睛吗4.在水里真的能睁开眼睛吗在水下不戴泳镜可以睁开眼睛游泳吗可以啊你可以先在脸盆里头练习。每天洗脸的时候。把脸埋进水里。然后慢慢的。一次比一次张开更多的眼皮。相信自己会成功的。。。游泳的时候

清朝说的披甲人是什么
综合百科清朝说的披甲人是什么清朝说的披甲人是一种帮助清王朝镇守边疆的降人,也是战士的一种,披甲人顾名思义,就是披着铠甲之人,虽说是战士,但和正规的战士又有些区别,其可根据不同时代的要求成为不同的身份。且披甲人是属于清朝八旗制度下的核心之一,因为八旗制度的核心就是以旗统军,以旗统民,旗丁按

五菱宏光s用什么汽油好,五菱宏光s加什么油
综合百科本文目录1.五菱宏光s加什么油2.五菱宏光s坐垫七件套3.五菱宏光加什么油92还是954.五菱宏光s到底该加92号汽油还是95号汽油五菱宏光s加什么油五菱洪光加92号汽油就能满足要求。可以加的最低等级的汽油会在车的油箱旁边标明。根据上述说明或维护手册中的规定添加相应等级的汽油。汽

减震器越硬越好,减震器硬的好还是软的好
综合百科本文目录1.减震器硬的好还是软的好2.减震器越硬越好吗3.避震器越硬越好吗4.电动车避震器软的好还是硬的好呢减震器硬的好还是软的好没有严格意义上的谁好谁坏,减震的软硬是由车辆的调教决定的,取决于减震器对弹簧弹力及阻尼器的阻尼力之间的匹配调教。其软硬效果主要也是因人而异,有些人可能

起泡胶的玩法,液态玻璃起泡胶怎么玩
综合百科液态玻璃起泡胶怎么玩先把液态玻璃起泡胶放在网格上面停留十几秒,然后开始慢慢往上拉,最后用手去捏就会有炸耳朵的声音。起泡胶是一种娱乐用品,它拥有绵软、起泡等特点。组成起泡胶的材料是胶水、水、容器、剃须、泡硼砂水、甘油,其中甘油和水不要加太多。 起泡胶的玩法1、将起泡胶像和面一样反

单反的镜头有什么用,单反镜头分类及作用是什么
综合百科本文目录1.单反相机的镜头起到了什么作用2.单反相机镜头各有什么用处3.单反相机镜头对相机有什么作用4.单反相机镜头有什么用单反相机的镜头起到了什么作用1:单反:单镜头反光 2:镜头的作用就是取景并根据摄入镜头的光线亮度将景色真实的反映到单反相机的机身五菱镜和反光镜上。单反相机镜

消防的四懂四会内容是什么,消防安全四懂四会的内容是什么
综合百科消防安全四懂四会的内容是什么消防安全知识四懂指:懂得岗位火灾的危险性;懂得预防火灾的措施;懂得扑救火灾的方法;懂得逃生疏散的方法。四会指:会使用消防器材;会报火警;会扑救初起火灾;会组织疏散逃生。四懂四会是加强对可燃物质的管理,提高人民消防意识和能力的一种宣传方式和考核标准。四懂








