绝对值的几何意义
发布:小编
绝对值的几何意义
1、绝对值的几何意义:一个数的绝对值在数轴上表示这个数的点到原点的距离。
2、数轴的存在,将基本的有理数表示与基本的几何图形直线结合了起来,把每一个数字变成了点。而数字绝对值具有的非负性,与直线上两点间的距离是一致的。
3、绝对值的含义是表示该数的点与原点之间的距离,其实将其意义再扩展一下,就是表示两点之间的距离,并不一定强调与原点的距离。
绝对值的几何意义
绝对值的几何意义是一个数距离原点的距离,无论该数是正数还是负数,其绝对值代表了它与原点的距离。以下是对绝对值几何意义的详细描述:
1.数轴上的距离
绝对值可以通过数轴来理解。在数轴上,原点表示0,正数表示向右移动,负数表示向左移动。一个数的绝对值就是它与原点的距离。例如,|-3|=3,表示-3与原点的距离为3。
2.点到原点的距离
在平面几何中,绝对值可以被解释为一个点到原点的距离。原点是平面上的(0,0),任意一点的坐标可以表示为(x,y)。这个点到原点的距离可以用绝对值来表示,即√(x^2+y^2)。
3.几何图形的边长
在几何图形中,绝对值可以表示边长或向量的模长。例如,在直角坐标系中,一个矩形的边长可以用绝对值表示,而不受矩形的位置或方向的影响。同样地,一个向量的模长也可以用绝对值来表示。
4.距离和大小的概念
绝对值还可以用来比较两个数的大小关系。无论正数还是负数,它们的绝对值越大表示它们与原点的距离越远,即数的绝对值大小与数的距离有着直接的关系。

5.应用于解析几何和物理学
绝对值在解析几何和物理学中广泛应用。在解析几何中,绝对值用于计算两点之间的距离、判断点是否在某个区域内等。在物理学中,绝对值用于计算物体的速度、加速度等物理量的大小。
6.绝对值与三角函数的关系
绝对值与三角函数也存在一定的关系。例如,sinθ和cosθ的绝对值都不会超过1,它们表示了一个角度的坐标在单位圆上的投影长度。在三角函数的图像中,绝对值可以代表波峰与波谷之间的距离,或者代表振幅的大小。
总结:绝对值的几何意义是一个数距离原点的距离,可以通过数轴表示,也可以解释为一个点到原点的距离。在几何图形中,绝对值可以表示边长或向量的模长。绝对值还可以用于比较数的大小关系,应用于解析几何和物理学中。此外,绝对值与三角函数也存在一定的关系。绝对值在数学和物理学中具有广泛的应用。
绝对值的几何意义
绝对值的几何意义:在数轴上,一个数到原点的距离叫做该数的绝对值。|a-b|表示数轴上表示a的点和表示b的点的距离。
绝对值的意义
几何意义
在数轴上,一个数到原点的距离叫做该数的绝对值。|a-b|表示数轴上表示a的点和表示b的点的距离。
应用:指在数轴上5与原点的距离,这个距离是5,所以5的绝对值是5。同样,|-5|指在数轴上表示-5与原点的距离,这个距离是5,所以-5的绝对值也是5。|-3+2|指数轴上-3和-2点的距离,这个式子值是1。同样|3-2|也表示3和2点的距离。
代数意义
非负数(正数和0)的绝对值是它本身,非正数(负数)的绝对值是它的相反数。
实数a的绝对值永远是非负数,即|a|≥0。互为相反数的两个数的绝对值相等,即|a|=|-a|(因为在数轴上它们到原点的距离相等)。
若a为正数,则满足|x|=a的x有两个值±a,如|x|=3,则x=±3。
绝对值的典型例题
阅读材料:我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
(1)若|x﹣3|=|x+1|,则x=
(2)式子|x﹣3|+|x+1|的最小值为
(3)若|x﹣3|+|x+1|=7,求x的值.
答案:(1)x=1(2)4(3)x=9/2或x=﹣5/2
以上就是关于绝对值的几何意义的全部内容,以及绝对值的几何意义的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【推酷网】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。
大家都在看

犯罪预备会减轻处罚吗,犯罪预备的处罚原则有哪些
综合百科犯罪预备的处罚原则有哪些犯罪预备亦称预备犯。是为犯罪准备工具、制造条件的行为。犯罪预备的处罚以比照既遂犯从轻、减轻处罚或者免除处罚为原则。考虑到犯罪预备行为虽然尚未直接侵害犯罪客体,但已经使犯罪客体面临即将实现的现实危险,因而同样具有社会危害性。因此对于预备犯应当追究刑事责任。同

数码相机如何调节光圈,数码相机如何手动控制光圈和快门速度
综合百科数码相机如何调节光圈数码相机调节光圈的方法:将相机的拍摄档调整到A档,A档代表光圈优先档位,就可以对光圈进行调整,自找到相机的肩屏,一般拨动肩屏可以调整光圈大小,控制进光量,调节明暗。光圈是一个用来控制光线透过镜头,进入机身内感光面光量的装置,它通常是在镜头内。表达光圈大小是用F
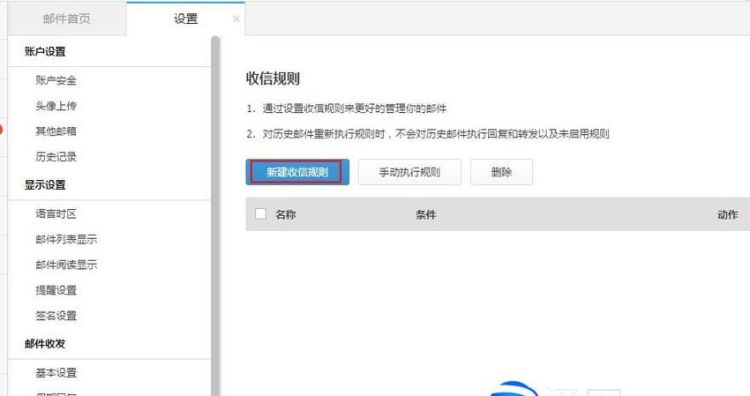
阿里云邮箱如何改密码,阿里云邮箱如何改密码登录
综合百科本文目录1.阿里云邮箱如何改密码登录2.阿里云企业邮箱官网3.手机版阿里邮箱怎么改密码登录4.阿里云邮箱怎么找回密码登录阿里云邮箱如何改密码登录阿里云邮箱改密码的方法如下:1、登录阿里云邮箱。2、点击进入页面右上角的用户中心。3、在用户中心页面下方找到“登录密码”点击“修改”。4

dx格式是什么意思,尼康的DX格式是什么意思
综合百科dx格式是什么意思DX格式是属于APS-C画幅单反相机的,DX是指尼康旗下的专门为APS-C尺寸设计的传感器,在实际使用中所有的镜头的焦段都要要乘以机身1.5的系数,之后实际的焦距就是全画幅的焦距。DX镜头不可用于传统胶片相机以及尼康新推出的FX格式的全幅数码单反D3相机。DX镜

被欺骗感情的句子,关于被感情欺骗的说说
综合百科关于被感情欺骗的说说这虚假的爱情里,我的幸福到最后终成空。你说得没错,以前的我太天真了才会被你欺骗,现在不会了,因为你不值得。痴情的人,统统被无情的人秒杀了。骗人好简单,骗自己。好难。 被欺骗感情的句子被欺骗感情的句子1.于我而言,酒前酒后无异,只是借助酒精我能欺骗自己,那些悲

快大型肉鸡有哪几种,一般我们常说的大肉食鸡包括哪些品种
综合百科本文目录1.一般我们常说的大肉食鸡包括哪些品种呢2.鸡在我国的驯养至少有多少年历史3.有哪些肉鸡品种属于快大型品种4.大型鸡品种有哪些图片一般我们常说的大肉食鸡包括哪些品种呢大肉食指的就是白羽肉鸡,也就是快大型肉鸡,通常有这几个品种,艾拔益加(AA、AA+)、艾维茵、罗斯、科宝等

索尼单反怎么手动对焦,如何对单反相机的对焦进行设置呢
综合百科索尼单反怎么手动对焦索尼单反手动对焦步骤如下:将机身的A/M切换,放到M档,然后转动镜头前端的对焦环,即可进行手动对焦。索尼是日本一家全球知名的大型综合性跨国企业集团。总部设于日本东京都港区港南1-7-1。索尼是世界视听、电子游戏、通讯产品和信息技术等领域的先导者,是世界最早便携

富秦家乐卡一万元每月利息多少,陕西信合家乐卡贷款利率是多少
综合百科本文目录1.银行的年利率怎么算2.家乐卡最多可以贷几年3.信合家乐卡贷款是怎么计息的4.富秦家乐卡一万元每月利息多少银行的年利率怎么算问题一:如何计算银行存款利率 一、计算利息的基本公式 储蓄存款利息计算的基本公式为:利息=本金×存期×利率 。(一)活期0.36一年36元。 (二

腾讯doki是什么意思,doki是什么意思梗
综合百科本文目录1.doki是什么意思梗2.怎么加入doki3.doki是什么意思4.doki怎么读doki是什么意思梗1、doki是腾讯视频里面专为明星鼓励加油的地方,在这里可以搜索查看到所有入驻的明星,选择自己心仪的偶像,即可选取不同的方式为其鼓气加油,成为该偶像在腾讯视频里的粉丝。
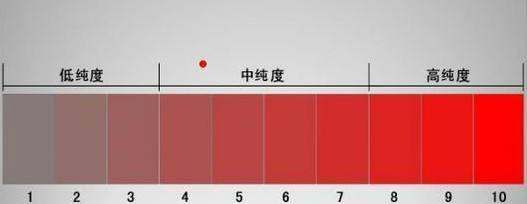
什么是色彩的纯度
综合百科什么是色彩的纯度色彩纯度,是指原色在色彩中所占据的百分比。纯度用来表现色彩的浓淡和深浅。纯度是深色、浅色等色彩鲜艳度的判断标准。纯度最高的色彩就是原色,随着纯度的降低,色彩就会变淡。纯度降到最低就失去色相,变为无彩色,也就是黑色、白色和灰色。彩色系中,常用彩度或者饱和度表示,而黑

50定焦镜头可以拍风景
综合百科50定焦镜头可以拍风景吗?50定焦镜头可以拍风景,人眼的单眼视角相当于全画幅50mm镜头,双眼相当于全画幅35mm镜头。所以把50mm左右的镜头叫做标准镜头,35mm以下的叫做广角镜头。广角镜头透视感强,适合拍摄风景,但是畸变也严重,拍摄人像和建筑很容易发现畸变。50mm镜头符合

美到极致的意思是什么意思,美出天际是什么意思
综合百科本文目录1.美出天际是什么意思2.因为娓致美到极致的意思3.美到极致的意思4.美到极致的意思是什么呢美出天际是什么意思美出天际的意思是,人或风景非常美,美的无法形容,普天之下已经找不到这么美得了,这个词可以用来形容人的漂亮,真心在帮你期待采纳,因为娓致美到极致的意思因为娓致,美到







